| 쉽게 설명하는 알고리즘 시리즈 |
|---|
| 1. Z Algorithm |
| 2. Manacher’s Algorithm |
이번 시간에는 Manacher’s 알고리즘을 소개하겠습니다.
Manacher’s 알고리즘이란?
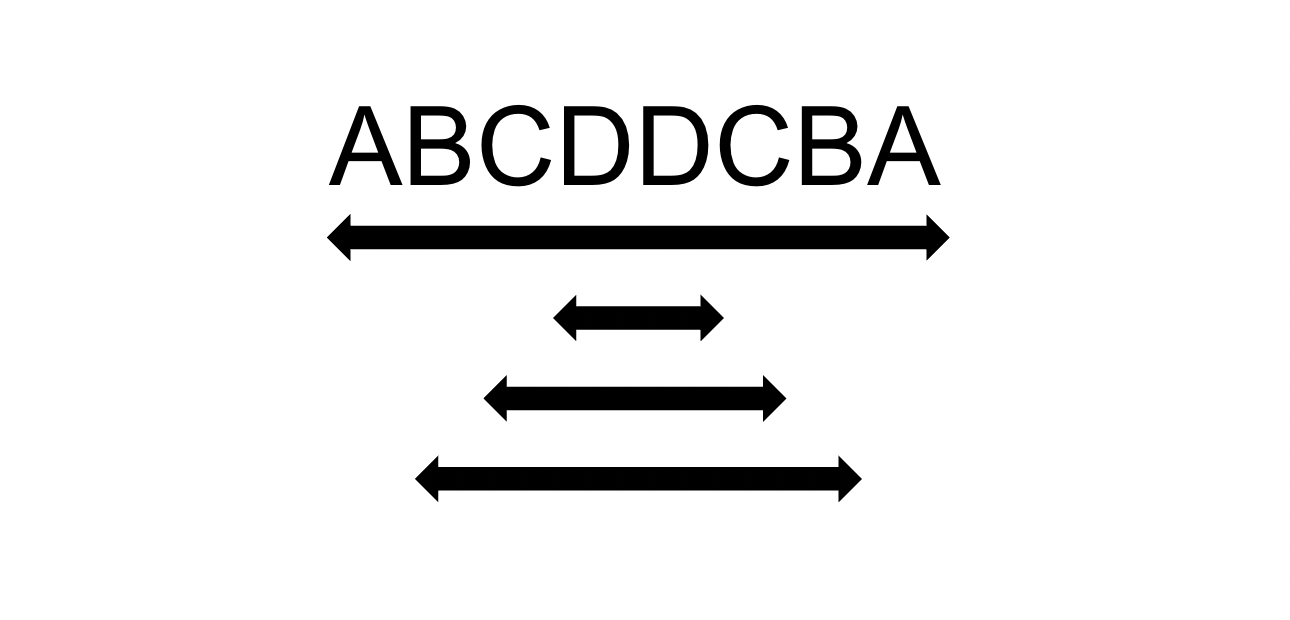
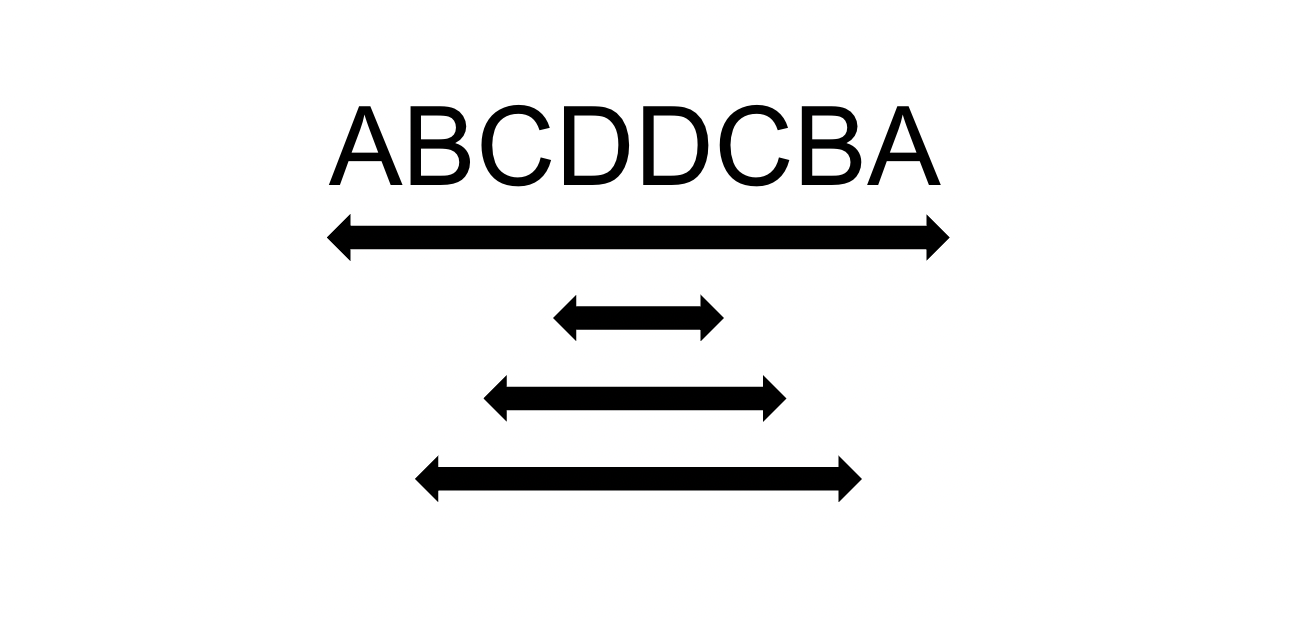
Manacher’s 알고리즘은 Glenn K. Manacher가 발명한 문자열에서 가장 긴 회문 부분 문자열을 찾는 데 사용되는 알고리즘으로, O(N)의 선형 시간 복잡도를 가집니다.
회문은 앞에서 읽으나 뒤에서 읽으나 똑같은 문자열로, 예를 들어 “기러기”, “토마토”, “스위스”, “우영우” 등이 있습니다.
코드를 보며 접근 방식을 하나씩 이해해 봅시다.
구현
먼저 무차별 대입 방식부터 살펴보겠습니다.
3개의 중첩 루프를 사용해 포인터 i와 j 사이의 구간을 모두 검사하여 문자열이 회문인지 확인합니다.
fun bruteForce(str: String): String {
var maxLength = 1
var start = 0
// 포인터 i와 j 사이의 문자열이 회문인지 검사합니다.
for (i in str.indices) {
for (j in i until str.length) {
// 검사할 문자열의 길이 (i와 j의 간격)
val range = j - i + 1
var isPalindrome = true
// 회문은 앞 뒤를 같이 검사하기 때문에 간격의 반만 반복합니다.
for (k in 0 until range / 2) {
// 만약 대상 문자열의 앞 뒤가 같지 않다면, 회문이 아니므로 바로 검사를 종료합니다.
if (str[i + k] != str[j - k]) {
isPalindrome = false
break
}
}
// 대상 문자열이 회문이고 현재 가장 긴 회문 부분 문자열보다 길다면, 가장 긴 회문 부분 문자열을 현재 문자열로 설정합니다.
if (isPalindrome && range > maxLength) {
start = i
maxLength = range
}
}
}
return str.substring(start, start + maxLength)
}
세 개의 for 루프를 사용하므로 시간 복잡도는 O(N^3)입니다.
이대로는 너무 느리니, 이미 반복한 부분, 즉 하위 문제의 결과를 저장하여 동적 프로그래밍으로 시간 복잡도를 줄여 보도록 하겠습니다.
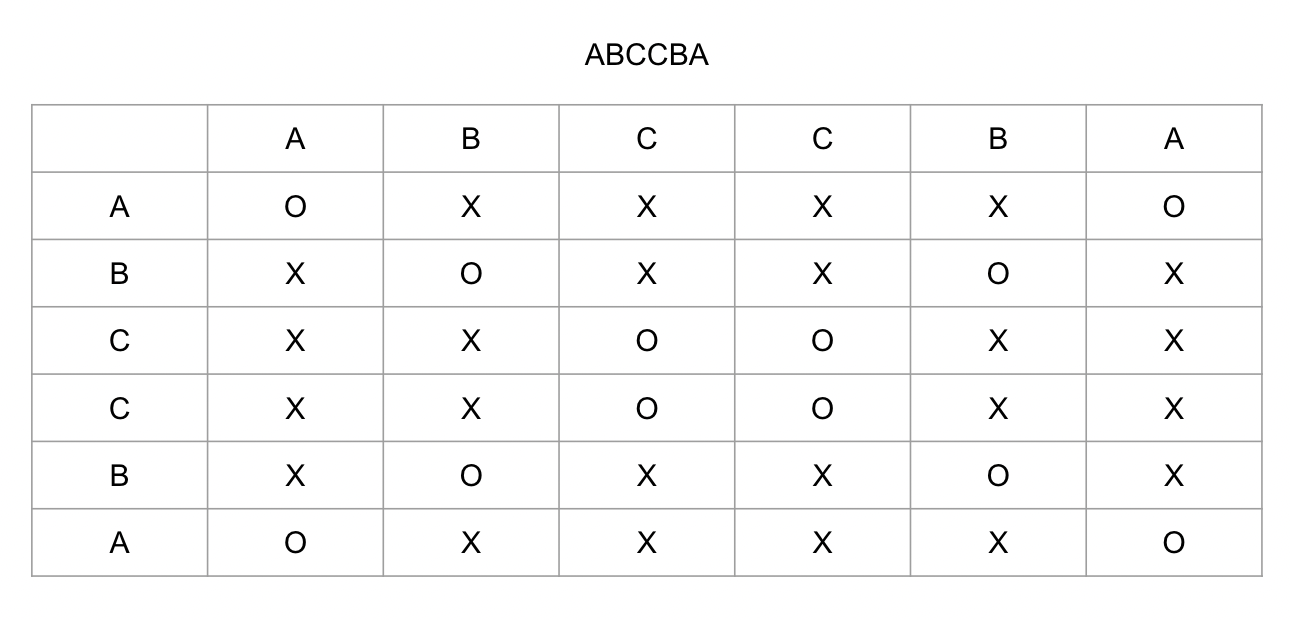
부울 배열 table에 하위 문자열의 회문 여부를 저장하여 이전 결과를 사용해 회문인지 판단합니다.
fun dp(str: String): String {
val len = str.length
// 회문 여부를 저장할 n x n 크기의 부울 배열
val table = Array(len) { BooleanArray(len) }
// 문자열의 각 문자는 모두 길이가 1인 회문이므로, 단일 문자를 모두 true로 설정합니다.
for (i in str.indices) {
table[i][i] = true
}
var start = 0
var maxLength = 1
// 길이가 짝수인 회문은 항상 길이 2의 회문으로 시작하므로, 빠른 검색을 위하여 길이가 2인 회문을 미리 체크합니다.
// 길이가 홀수인 회문은 위에서 체크한 결과를 사용합니다.
for (i in 0 until len - 1) {
if (str[i] == str[i + 1]) {
table[i][i + 1] = true
start = i
maxLength = 2
}
}
// 길이가 1인 회문과 길이가 2인 회문을 체크했기 때문에, 현재 루프에서는 길이가 3 이상인 회문만 체크합니다.
for (i in 3..len) {
// 회문은 앞 뒤를 같이 검사하기 때문에 간격의 반만 반복합니다.
for (j in 0 until len - i + 1) {
val range = j + i - 1
// table[j + 1][range - 1]은 검사하려고 하는 문자열의 부분 문자열의 회문 여부를 나타냅니다.
// abba라는 문자열을 검사한다고 가정할 때, 위에서 이미 길이 2인 회문이 모두 체크되었기 때문에 table을 확인하기만 하면 가운데 문자열인 bb를 다시 검증할 필요가 없습니다.
// 만약 부분 문자열이 회문이라면, 이 문자열도 회문일 가능성이 있으므로 이 문자열도 검사하여 table에 결과를 체크합니다.
// 다음 반복에서는 지금 저장한 결과를 사용하여 부분 문자열을 검증할 수 있습니다.
if (table[j + 1][range - 1] && str[j] == str[range]) {
table[j][range] = true
if (i > maxLength) {
start = j
maxLength = i
}
}
}
}
return str.substring(start, start + maxLength)
}
이중 반복이므로 시간 복잡도는 O(N^2)입니다.
그렇다면 Manacher’s Algorithm은 어떤 식으로 이 문제를 해결할까요?
동적 프로그래밍 알고리즘의 예시처럼 우리는 이전에 확인한 결과로 다음 회문의 유효성을 검증할 수 있습니다.
위의 알고리즘에서는 짝수의 경우에는 항상 가운데의 길이 2의 회문을 검증해야 했지만, 홀수의 경우에는 그럴 필요가 없었습니다.
그렇다면, 문자열을 홀수라고 가정했을 때, 짝수 번은 건너뛰고 홀수 번의 문자열만 확인하면 되지 않을까요?
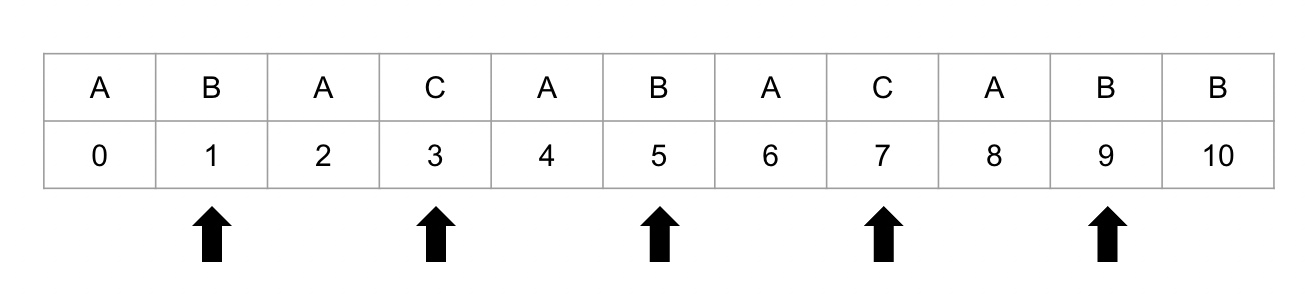
문자열의 왼쪽부터 시작하여 가장 긴 회문을 찾고, 회문의 끝 (가장 오른쪽의 하위 회문) 위치를 저장하여 ‘대칭 위치’를 사용하여 회문을 검증합니다.
자세한 내용은 구현된 코드와 함께 설명하겠습니다.
fun manachersAlgorithm(str: String): String {
// 앞 뒤의 구분 문자 및 홀수 길이 문자열을 위한 특수 문자를 삽입하기 때문에 배열의 길이는 문자열 * 2 + 3입니다.
val length = str.length * 2 + 3
val charArray = CharArray(length)
// 문자열의 끝 부분의 처리를 막기 위해 앞 뒤에 구분 문자를 추가합니다.
charArray[0] = '^'
charArray[charArray.lastIndex] = '$'
var p = 1
// Manacher's Algorithm은 홀수 길이의 문자열에서만 작동하기 때문에, 문자열 사이에 특수 문자 '#'을 삽입해 항상 문자열이 홀수 길이가 될 수 있도록 합니다.
for (c in str) {
charArray[p++] = '#'
charArray[p++] = c
}
charArray[p] = '#'
var maxLength = 0
var start = 0
var center = 0
var maxRight = 0
val table = IntArray(length)
for (i in 1 until length - 1) {
// 현재 인덱스가 현재 가장 오른쪽의 하위 회문보다 작다면, 현재 인덱스는 검증된 회문 안에 있습니다.
if (i < maxRight) {
// 가장 오른쪽에서 현재 인덱스를 뺀 값 (즉, 검증된 회문의 중앙)과 현재 중앙값의 반대편에서 현재 인덱스를 뺀 값, 즉 대칭 위치에 저장된 값을 비교하여 작은 값을 저장합니다.
// 현재 인덱스에서 시작될 수 있는 회문은 최소 작은 값 '이상'의 길이이기 때문입니다.
table[i] = min(maxRight - i, table[center * 2 - i])
}
// 현재 위치와 대칭 위치를 비교하여 회문을 검증합니다.
while (charArray[i + table[i] + 1] == charArray[i - table[i] - 1]) {
table[i]++
}
// 검증된 회문의 가장 오른쪽 하위 회문이 현재의 가장 오른쪽 하위 회문보다 크다면, 중앙값과 가장 오른쪽 하위 회문 값을 업데이트합니다.
if (i + table[i] > maxRight) {
center = i
maxRight = i + table[i]
}
// 현재 최장 회문의 길이와 검증된 회문의 길이를 비교하여 업데이트합니다.
if (table[i] > maxLength) {
start = (i - table[i] - 1) / 2
maxLength = table[i]
}
}
return str.substring(start, start + maxLength)
}
코드 예제는 GitHub에서 확인하실 수 있습니다.
연습 문제
가장 긴 회문 문자열을 구하는 문제입니다. Manacher’s 알고리즘을 실습해 봅시다.